The second law states that the net force on an object is equal to the rate of change (that is, the derivative) of its linear momentum p in an inertial reference frame:
S for Science is a fabulous site in which wonderful facts and descriptions are available that are enough to amaze you. All the information available here is written in simplified language so that everyone can understand it. So one must read and gain knowledge from this site. Relax and enjoy the Spectacular Science.
Monday, May 27, 2013
Newton's Second Law of Motion
The second law states that the net force on an object is equal to the rate of change (that is, the derivative) of its linear momentum p in an inertial reference frame:


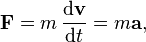
No comments:
Post a Comment